IPMAT 2024
Actual Question Paper
1. Let ABC be a triangle right-angled at B with AB = BC = 18. The area of largest rectangle that can be inscribed in this triangle and has B as one of the vertices is _________
2. The following table shows the number of employees and their median age in eight companies located in a district
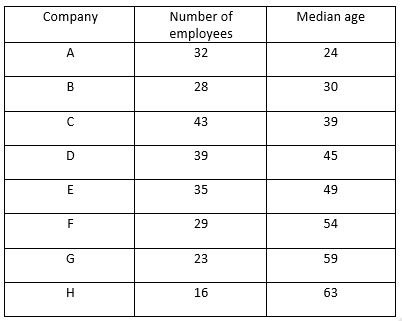
It is known that the age of all employees are integers. It is known that the age of every employee in A is strictly less than the age of every employee in B, the age of every employee in B is strictly less than the age of every employee in C,… the age of every employee in G is strictly less than the age of every employee in H.
In company F, the lowest possible sum of the ages of all employees is_______
4. The following table shows the number of employees and their median age in eight companies located in a district
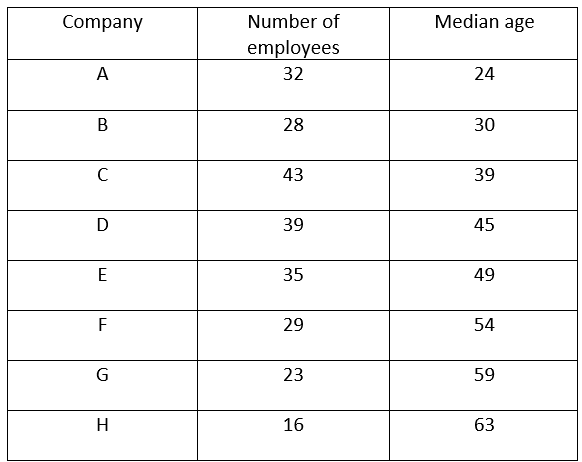
It is known that the age of all employees are integers. It is known that the age of every employee in A is strictly less than the age of every employee in B, the age of every employee in B is strictly less than the age of every employee in C,… the age of every employee in G is strictly less than the age of every employee in H.
The median age of employees across the eight companies is _________
5. The price of a chocolate is increased by x% and then reduced by x%. The new price is 96.76% of the original price. Then x is ___________
6. Person A borrows Rs. 4000 from another person B for a duration of 4 years. He borrows a portion of it at 3% simple interest per annum, while the rest at 4% simple interest per annum. If B gets Rs. 520 as total interest, then the amount A borrowed at 3% per annum in Rs. is
7. The following table shows the number of employees and their median age in eight companies located in a district
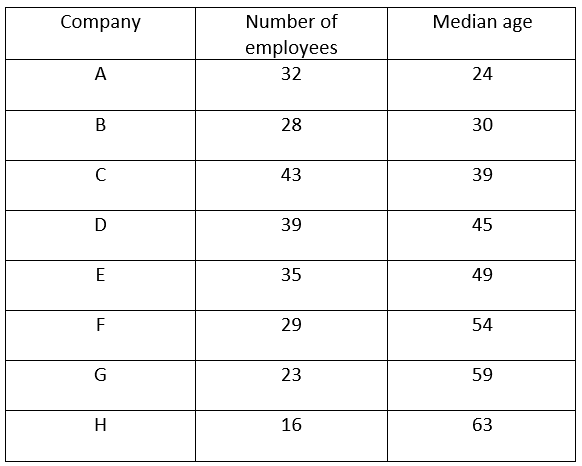
It is known that the age of all employees are integers. It is known that the age of every employee in A is strictly less than the age of every employee in B, the age of every employee in B is strictly less than the age of every employee in C,…, the age of every employee in G is strictly less than the age of every employee in H.
The highest possible age of an employee of company A is ________
8. If A=⎡⎣⎢x1y1z1x2y287y33⎤⎦⎥is a matrix such that the sum of all three elements along any now, column or diagonal are equal to each other, then the value of determinant of A is
9. The number of real solutions of equation (x2 – 15x + 55)(x2-5x+6) = 1 is
11. The number of factors of 1800 that are multiple of 6 is _________
12. In a group of 150 students, 52 like tea, 48 like juice and 62 like coffee. If each student in the group likes at least one among tea, juice and coffee, then the maximum number of students that like more than one drink is_________
13. A fruit seller has oranges, apples and bananas in the ration 3 : 6 : 7. If the number of oranges is a multiple of both 5 and 6, then the minimum number of fruits the seller has is_______
14. Let f and g be two function defined by f(x)=|(x+|x|)| and g(x)=1/x for x≠0. If f(a)+g(f(a))=13/6 for some real a. then the maximum possible vale of f(g(a)) is _________
15. The number of triangles with integer sides and with perimeter 15 is _______
16. Sagarika divides her savings of 10000 rupees to invest across two schemes A and B. Scheme A offers an interest rate of 10% per annum, compounded half-yearly, while scheme B offers a simple interest rate of 12% per annum. If at the end of first year, the value of her investment in scheme B exceeds the value of her investment in scheme A by 2310 rupees, then the total interest, in rupees, earned by Sagarika during the first or investment is
- A. 1100
- B. 1130
- C. 1111
- D. 1000
17. If the shortest distance of a given point to a given circle is 4 cm and the longest distance is 9 cm, then the radius of the circle is
- A. 2.5 cm
- B. 5 cm or 13 cm
- C. 2.5 cm or 6.5 cm
- D. 6.5 cm
18. The terms of a geometric progression are real and positive. If the p-th term of the progression is q and q-th term is p. then the algorithm of the first term is
A.
B.
C.
D.
- A. 20200
- B. 18400
- C. 19600
- D. 19200
- A. 2100 + 3100
- B. 3200
- C. 4100
- D. 2300
- A. 1.2
- B. 2.1
- C. 3.4
- D. 4.3
A.
B.
C.
D.
- A. 10 √3+1)
- B. 30
- C. 20 (√3+1)
- D. 15 (√5+1)
24. A fruit seller had a certain number of apples, bananas and oranges at the start of the day. The number of bananas was 10 more than the number of apples, and the total number of bananas and apples was a multiple of 11. She was able to sell 70% if apples, 60% of bananas, and 50% of oranges during the day. If she was able to sell 55% of the fruits she had at the start of the day. Then the minimum number of oranges she had at the start of the day was
- A. 190
- B. 210
- C. 220
- D. 180
25. A boat goes 96 km upstream in 8 hours and covers the same distance moving downstream in 6 hours. On the next day boat starts from point A, goes downstream for 1 hour, then upstream for 1 hour and repeats this four times, that is, 5 upstream and 5 downstream journeys. Then the boat would be
- A. 15 km downstream of A
- B. 20 km downstream of A
- B. 20 km downstream of A
- C. 22.5 km downstream of A
- D. 12.5 km downstream of A
26. The smallest possible number of students in a class if the girls in the class are less than 50% but more than 48% is
- A. 200
- B. 25
- C. 27
- D. 100
27. Let a =
- A. 7/2
- B. 5/2
- C. 8
- D. 5
28. If 5 boys and 3 girls randomly sit around a circular table, the probability that there will be at least one boy sitting between any two girls, is
- A. 1/3
- B. 1/4
- C. 2/7
- D. 1/7
- A. 2√7
- B. √10
- C. 2√5
- D. √7
- A. 1.5
- B. 2.6
- C. 3.4
- D. 4.2
- A. 1/7
- B. 2
- C. 1/5
- D. 1/2
- A. 4/5
- B. 2/5
- C. 20/21
- D. 5/4
33. In a survey of 500 people, it was found that 250 owned a 4-wheeler but not a 2-wheeler, 100 owned a 2-wheeler but not a 4-wheeler, and 100 owned neither a 4-wheeler nor a 2-wheeler. Then the number of people who owned both is
- A. 100
- B. 50
- C. 60
- D. 75
- A. 2065
- B. 1987
- C. 2025
- D. 2000
A.
B.
C.
D.
36. Let ABC be an equilateral triangle, with each side of length k. IF a circle is drawn with diameter AB, then the area of the portion of the triangle lying inside the circle is
- A. (3√3+π)(k2/6)
- B. (3√3-π)(k2/6)
- C. (3√3+π)(k2/24)
- D. (3√3-π)(k2/24)
- A. 10o
- B. 30o
- C. 15o
- D. 60o
- A. 1
- B. -1
- C. -7
- D. 7
39. Let n be the number of ways in which 20 identical balloons can be distributed among 5 girls and 3 boys such that everyone gets at least one balloon and no girls gets fewer ballons than a boy does. Then
- A. 9000 ≤ n < 10000
- B. 7000 ≤ n < 8000
- C. 8000 ≤ n < 9000
- D. 6000 ≤ n < 7000
40. The sum of a given infinite geometric progression is 80 and the sum of its first two terms is 35. Then the value of n for which the sum of its first n terms is closest to 100, is
- A. 6
- B. 4
- C. 7
- D. 5
Direction 41 – 45: In an election there were five constituencies S1, S2, S3, S4 and S5 with 20 voters each all of whom voted. Three parties A, B and C contested the elections.
The party that gets maximum number of votes in a constituency wins the seat. In every constituency there was a clear winner. The following additional information is available:
• Total number of votes obtained by A, B and C across all constituencies are 49, 35 and 16 respectively.
• S2 and S3 were won by C while A won only S1.
• Number of votes obtained by B in S1, S2, S3, S4 and S5 are distinct natural numbers in increasing order
41. Assume that A and C had formed an alliance and any voter who voted for either A or C would have voted for this alliance. Then the number of seats this alliance would have won is
- A. 5
- B. 3
- C. 4
- D. 2
42. The number of votes obtained by A in 28 S5 is
- A. 7
- B. 9
- C. 8
- D. 6
43. The constituency in which B got 28 lower number of votes compared to A and C is
- A. S4
- B. S3
- C. S2
- D. S1
44. The number of votes obtained by B in 29 S2 is
- A. 6
- B. 7
- C. 5
- D. 4
45. Comparing the number votes obtained by A across different constituencies, the lowest number of votes were in constituency
- A. S5
- B. S4
- C. S3
- D. S2
